はじめに:ハンドボールを遠くへ投げたい
本記事は久しぶりの勉強に関する記事です。
本記事のテーマはタイトル通り「投げたボールの軌道シミュレーション」です。
本記事と同様の内容をYouTubeにも投稿しています。
文章より動画が好みの方にオススメ↓
さて、皆さんは体育の授業でハンドボール投げをした経験はあるでしょうか?
私が通っていた学校では毎年、体力テストの一環でハンドボール投げが行われていました。
当時から運動が苦手だった私はハンドボール投げのスコアもイマイチでした。
そんな私が抱いた疑問は「最適な角度で投げれば、力が弱くても遠くに飛ばせるのでは?」です。
しかしながら当時の私は、ハンドボールを遠くに投げる力もなく、遠くに飛ぶ角度を知る知識もない…。
そこで当時の疑問「どの角度でボールを投げれば一番遠くに飛ぶのか?」を高校物理の知識を使って計算してみました。
私のようにハンドボール投げのスコアを上げたい人はぜひご覧ください!👀
本記事で考える「ボール投げ」の条件
本記事で扱う「ボール投げ」では以下を想定しています。
- ボールを前方に投げることを想定。
- 投げるスピードは15m/s(時速54km)と想定。
- 空気抵抗は無視する。
- 投げる角度は自由(0°~90°)
このときボールを遠くへ投げるのに最適な角度を計算します。
本記事では、数式だけ記しても面白くないので、PythonのライブラリMatplotlibを用いてボールの軌道をGIF画像にしてみました。
ボールの軌道はどのように決まるのか?
本章ではボールの軌道を計算するための数式について記します。
ややマニアックな話になるため、結果のみ確認したい人は次の章へどうぞ!
初速度を\(x\)成分と\(y\)成分に分解
本記事ではボールを初速度\(v\),角度\(θ\)で投げた場合の飛距離を計算します。
また、重力加速度を\(g(=9.8m^2/s)\)とします。
まず、ボールを投げた時、地面に落ちるまでの時間(滞空時間)を計算します。
角度\(θ\)で投げたボールの初速度を\(x\)成分と\(y\)成分に分解します。
\(v_x=v \,cosθ\)
\(v_y=v \,sinθ\)
鉛直方向つまり\(y\)方向の速度は、ボールに重力が働くため初速度からどんどん変化します。
一方で水平方向つまり\(x\)成分は等速運動です。
\(x(t)\)を\(t\)秒後のボールの\(x\)座標の値とすると、
\(x(t)=v \,cosθ\,t\)となります。
次に鉛直方向である\(y\)成分に注目するとボールには重力が働くため、\(t\)秒後における\(y\)座標の値は以下の通りです。
\(y(t)=v \,sinθ\,t-\frac{1}{2}gt^2\)
滞空時間を計算
この式を用いてボールの滞空時間を計算します。
ボールを投げた高さは\(0\),着地点の高さは\(0\)のため、\(y(t)=0\)を満たすような\(t\)(\(ただしt≠0\))を求めます。
\(y(t)=0\) とすると、
\(0=v \,sinθ\,t-\frac{1}{2}gt^2\) となり、
\(t=\frac{2v\,sinθ}{g}\)となります。
飛距離を計算
飛距離を計算するため、速度の\(x\)成分に滞空時間をかけると
飛距離 \(=v\,cosθ×\frac{2v\,sinθ}{g}\)
\(=\frac{2v^2\,cosθ\,sinθ}{g}\)
ここで2倍角の公式(\(sin2θ=2\,sinθ\,cosθ\))を使用して、
\(=\frac{v^2\,sin2θ}{g}\) と計算できます。
本記事では\(v=15m/s\)(時速\(54\)(km))・重力加速度\(g=9.8(m^2/s)\)と想定しているため、これらを代入すると飛距離は\(\frac{225}{9.8}\,sin2θ\)となります。
最適な角度は…?
よってボールの飛距離は角度\(θ\)によって変化することが分かります。
ここで本ブログのテーマである「ハンドボールを遠くに投げたい!」を考えてみます。
ボールの飛距離を最大にしたい時、\(sin2θ\)を最大にすればOKです。
ここで\(-1<sin2θ<1\) であるため、\(sin2θ=1\)のとき、
すなわち\(θ=\frac{π}{4}=45°\)のとき飛距離が最大になります!
以上より「投げる角度が\(45°\)の時、飛距離が最大となる」ことが分かりました!
計算における留意点
本検討における留意点を記しておきます。(他にもあるかも。)
- 空気抵抗を考慮していない
- 人間は投げる角度を変えた時、投げる速度も変わる可能性
30°で投げるときと60°で投げるとき、同じ速度で投げられるとは考えづらいです。
このように本検討では完全に現実世界を再現しているわけではないです。
しかしながら、ある程度参考にはなると思います。
ボールの軌道 アニメーション
ここまでは数式を中心とした説明でした。
本章では視覚的に分かりやすいよう、ボールの軌道のアニメーションを紹介します。
ボールを\(30°/45°/60°\)で投げた時のボールの軌道を見てみます。
\(15m/s\)(時速\(54km\))・角度\(30°\)の軌道
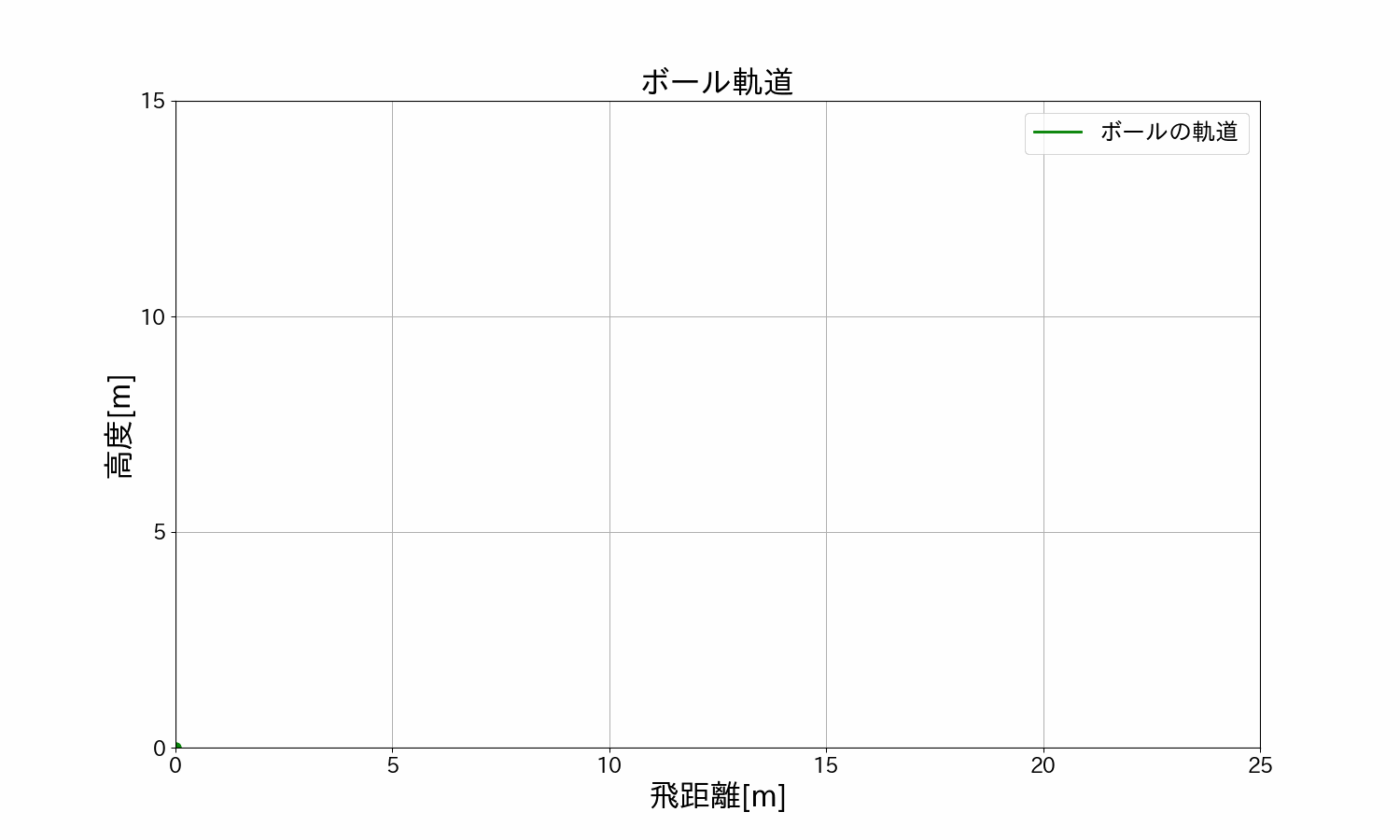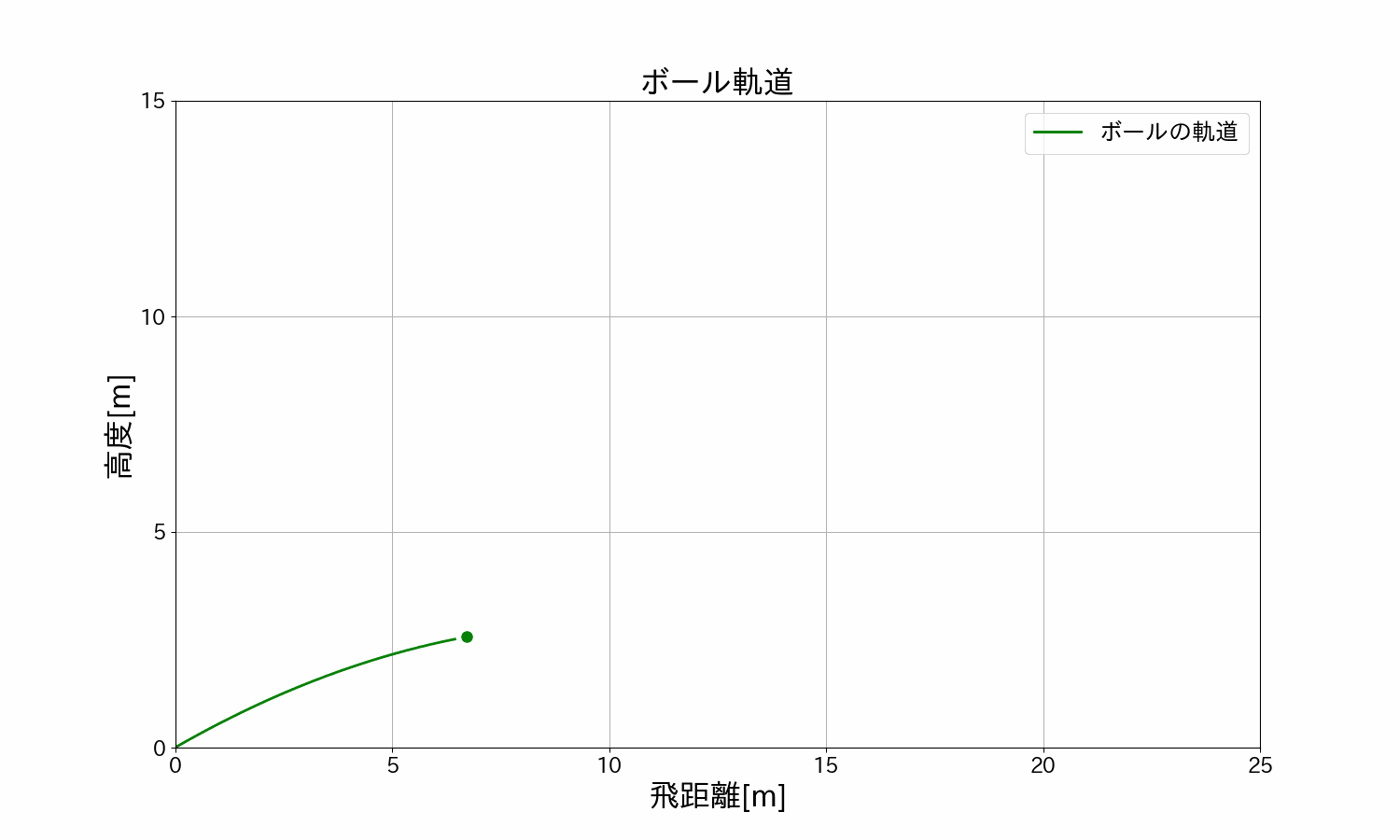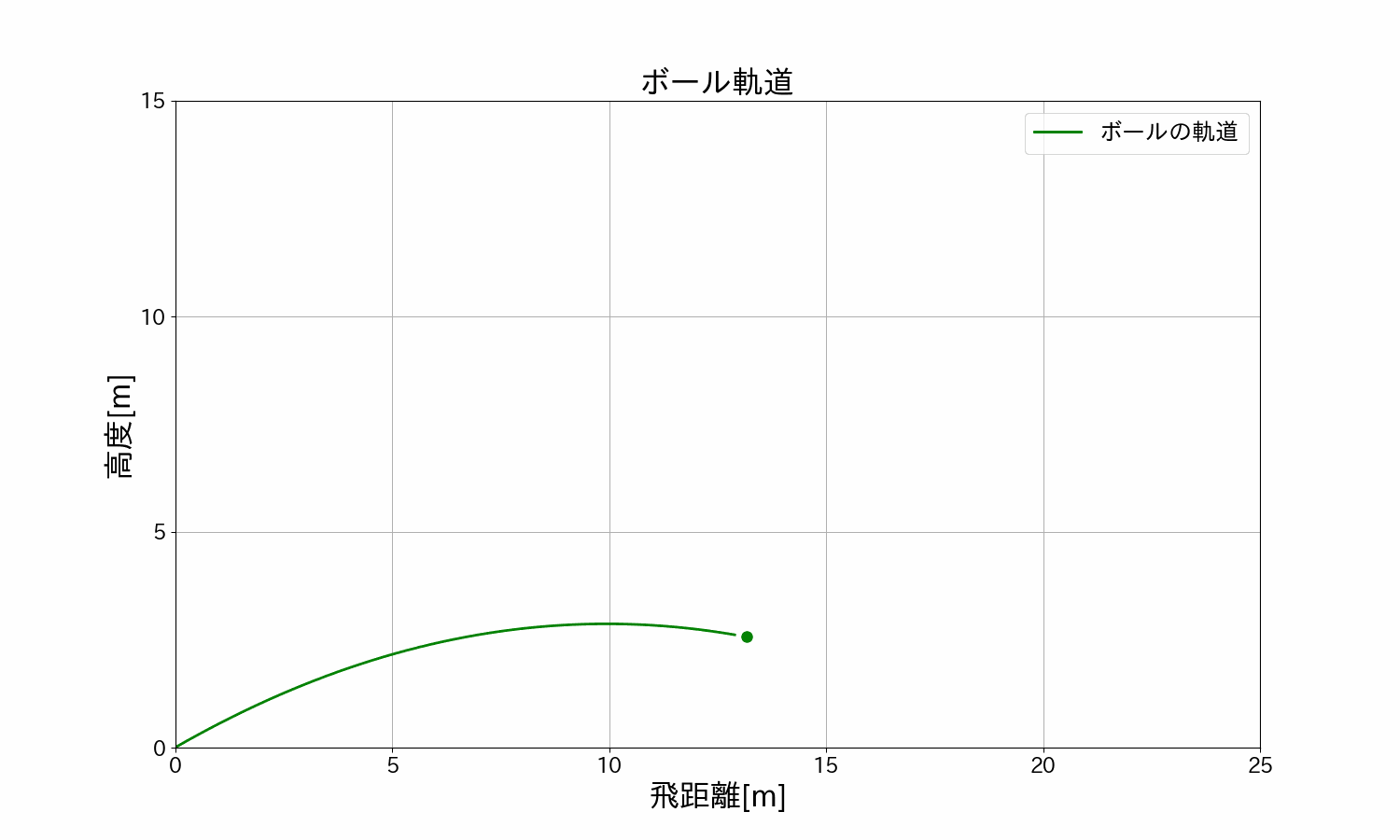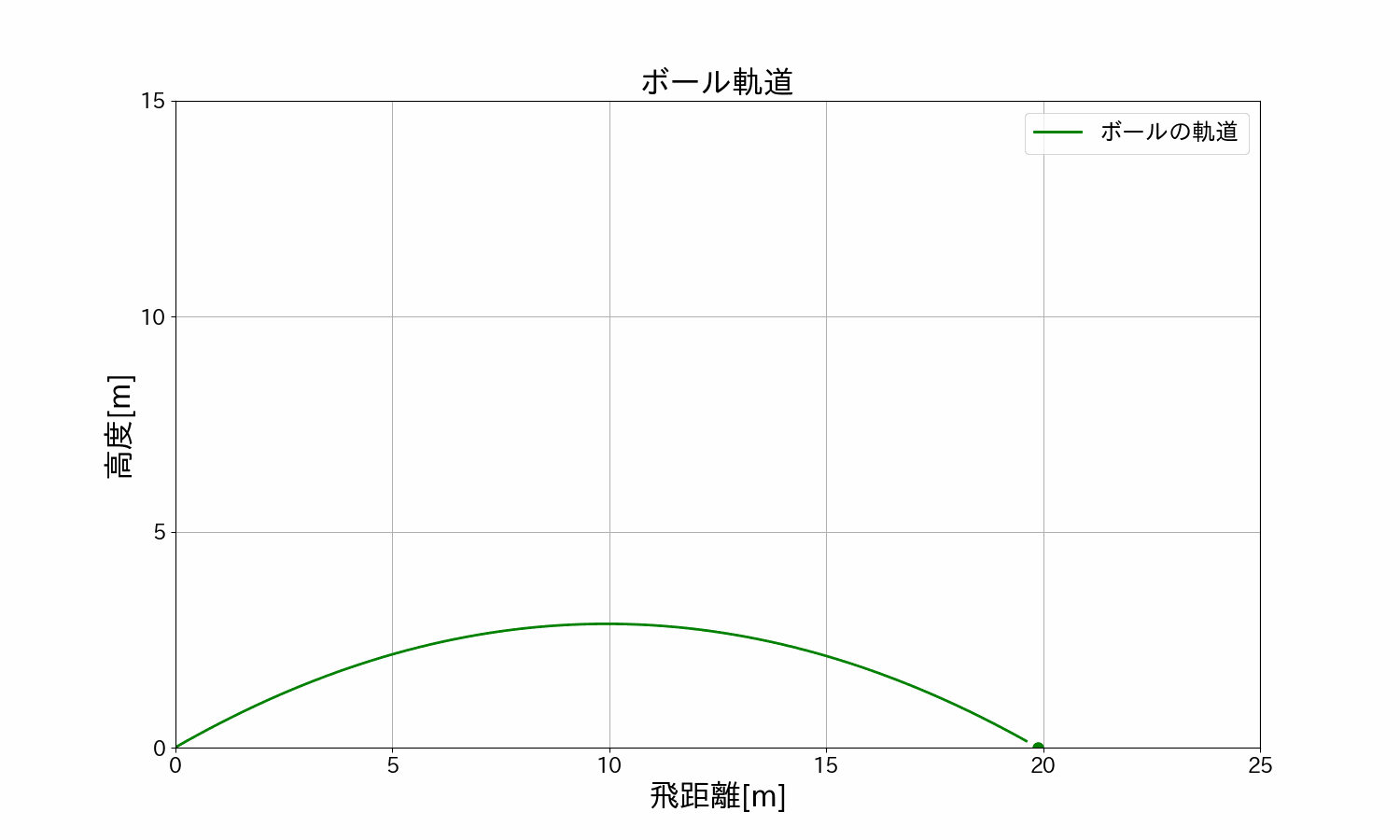
\(15m/s\)(時速\(54km\))・角度\(45°\)の軌道
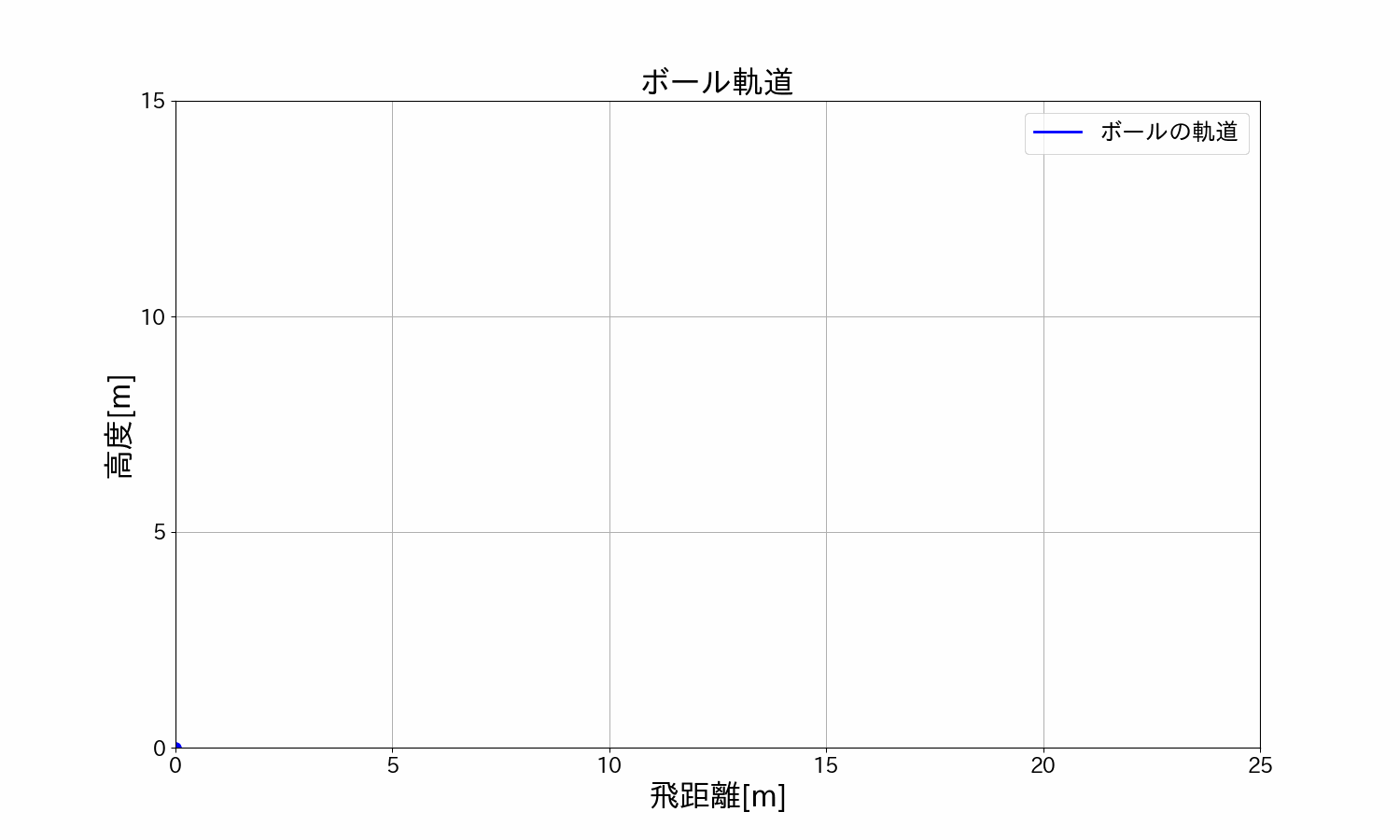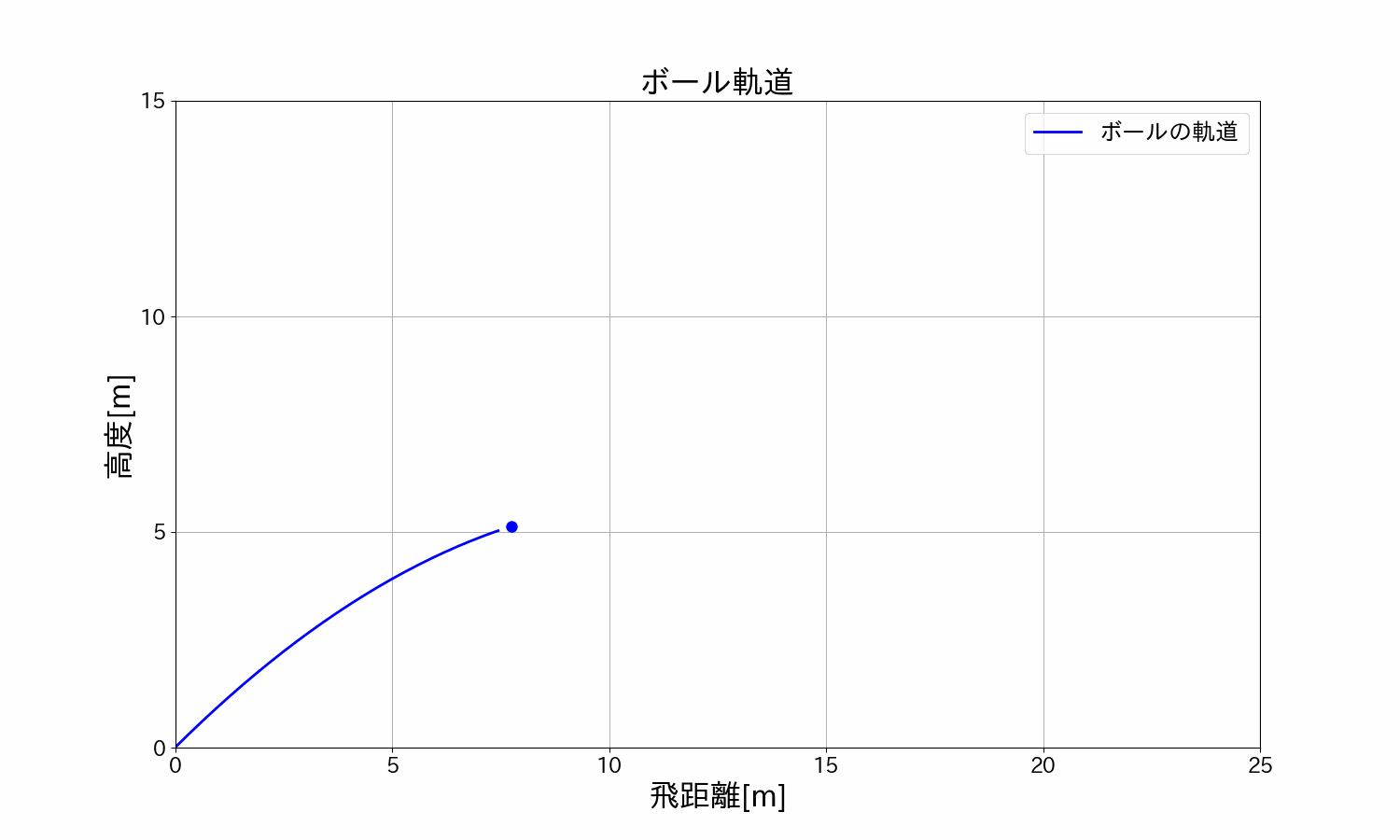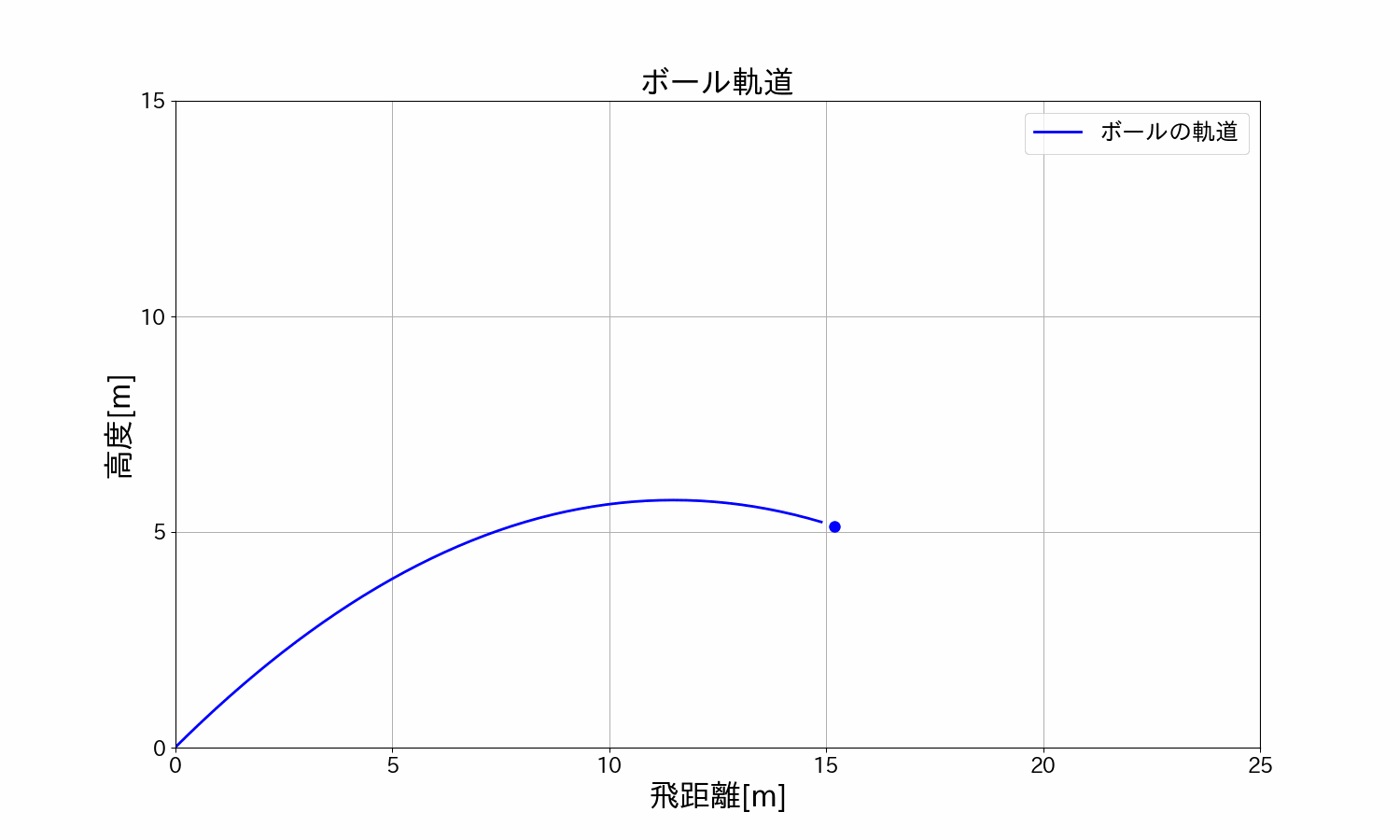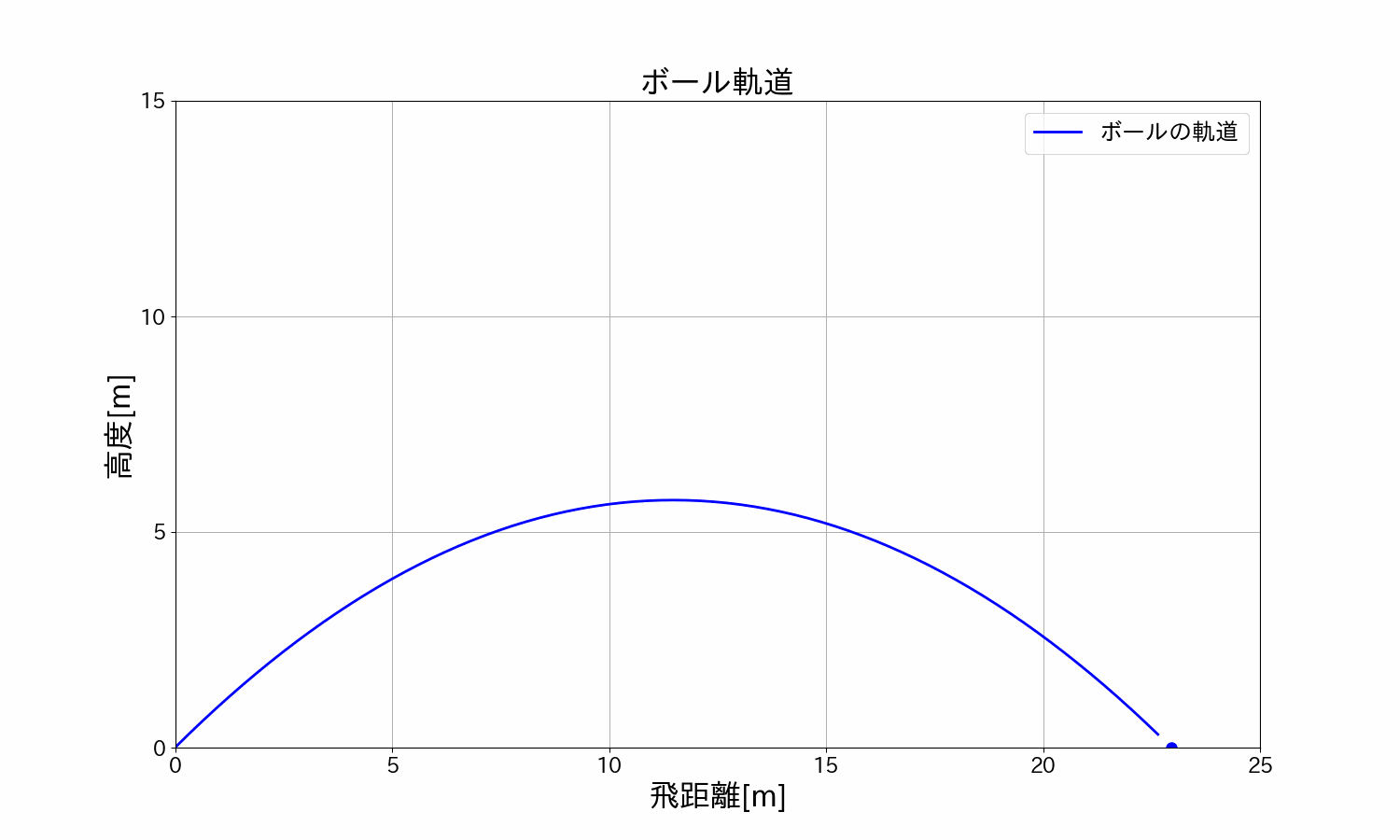
\(15m/s\)(時速\(54km\))・角度\(60°\)の軌道
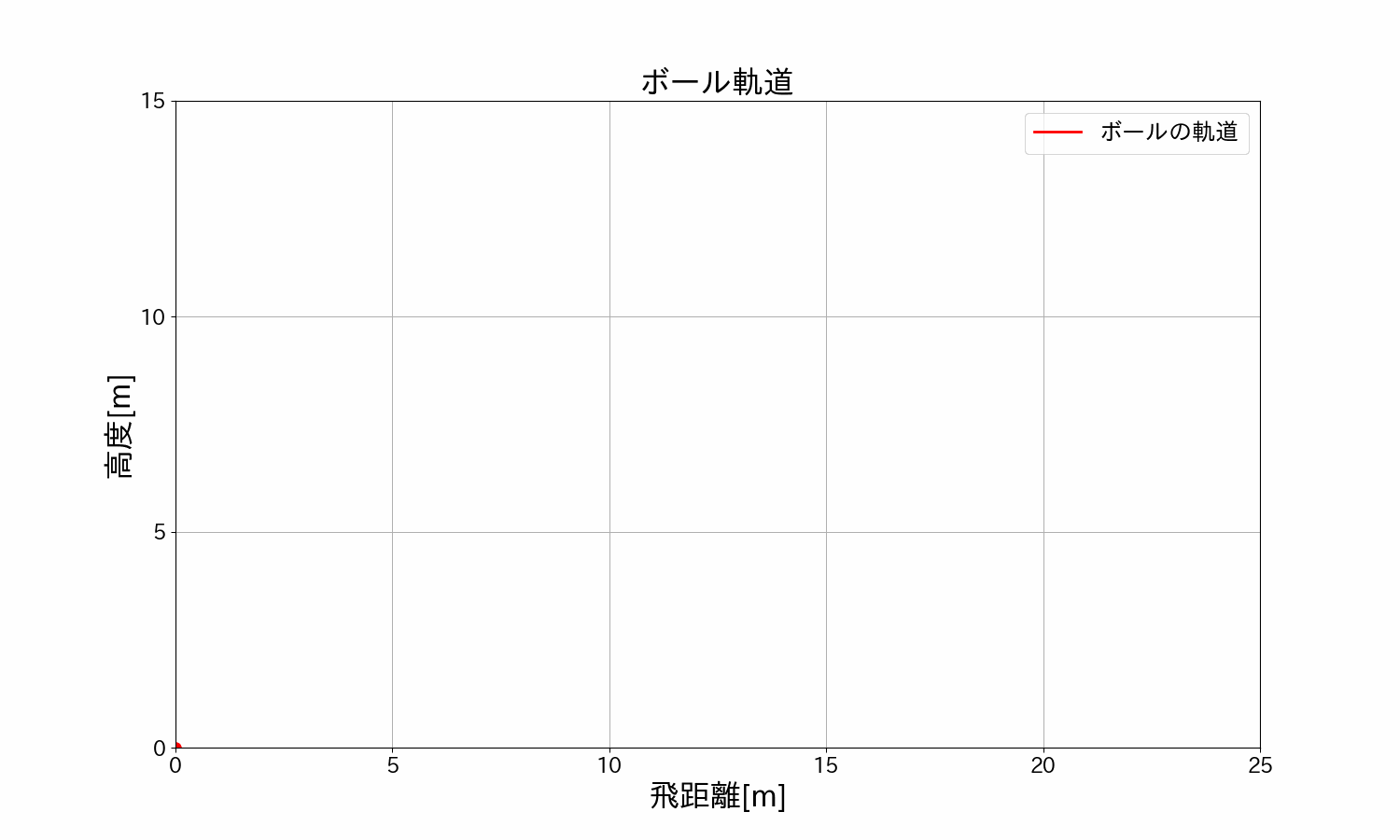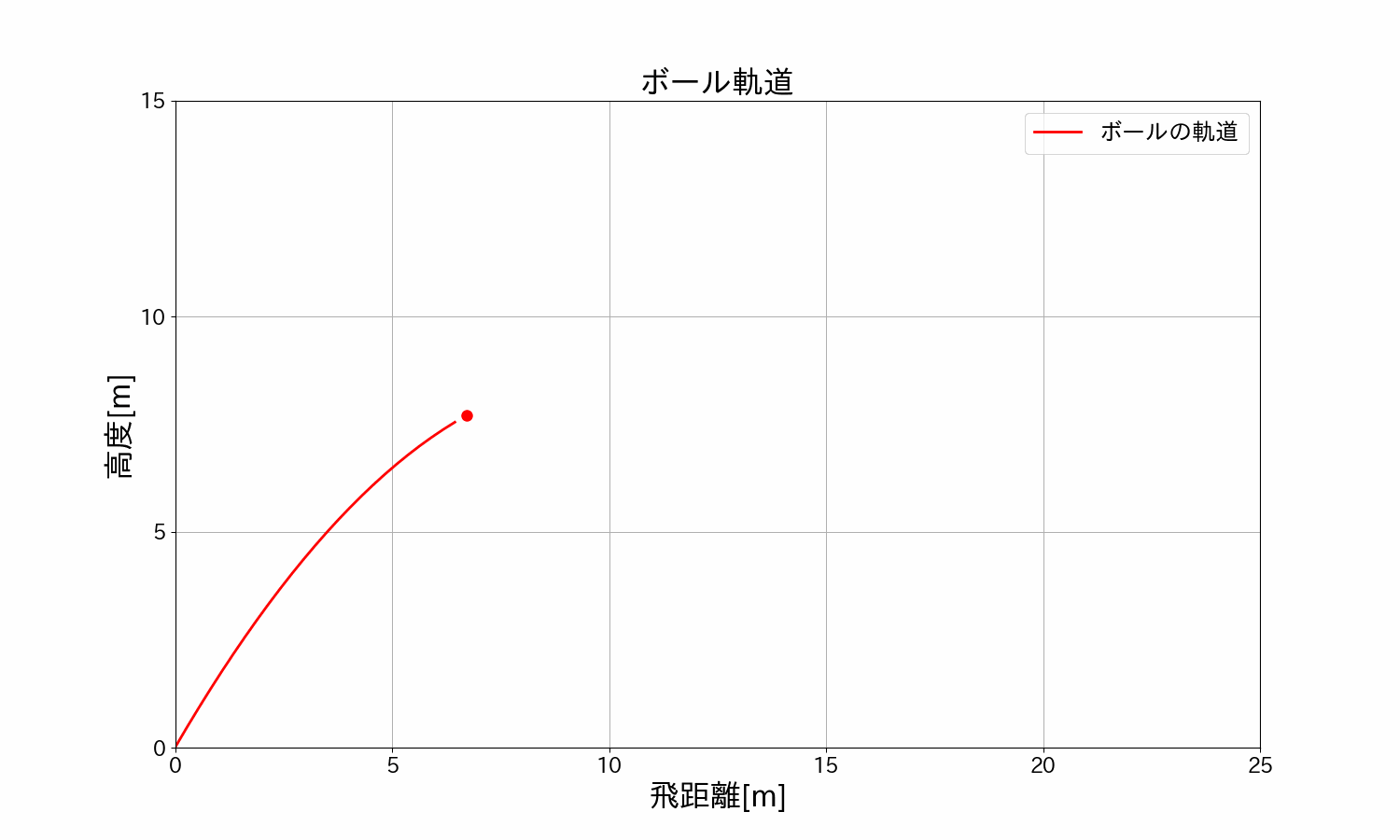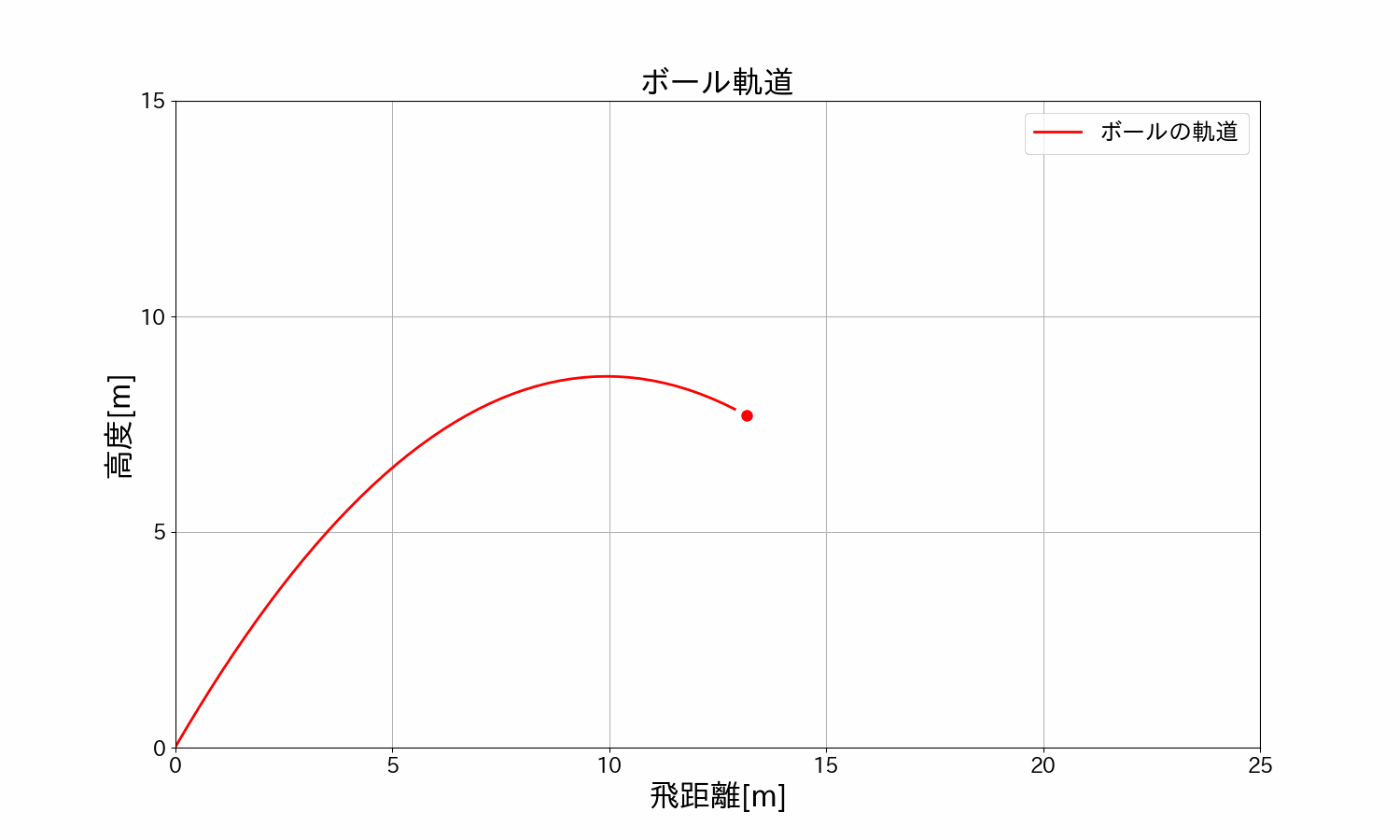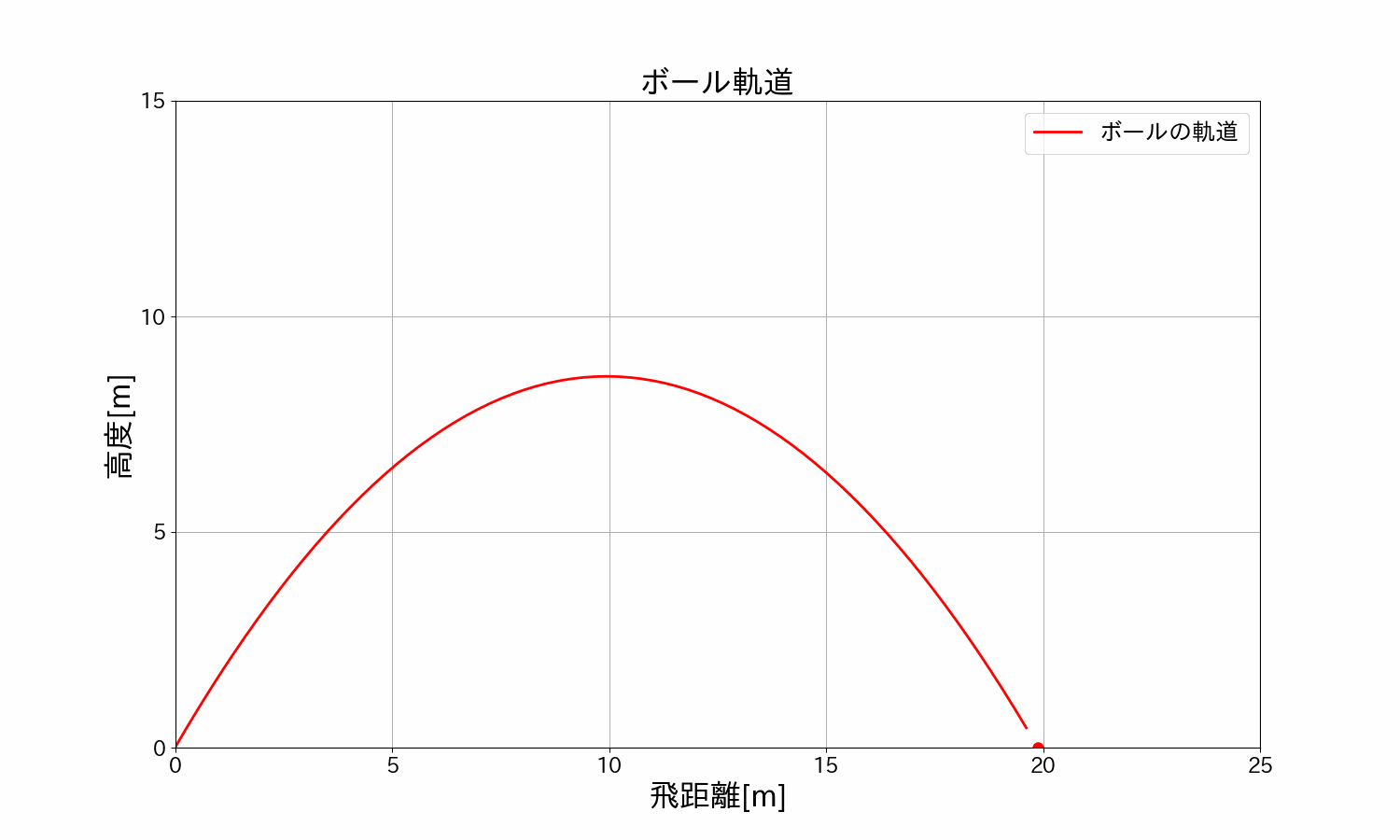
\(30°/45°/60°\)を重ねて比較
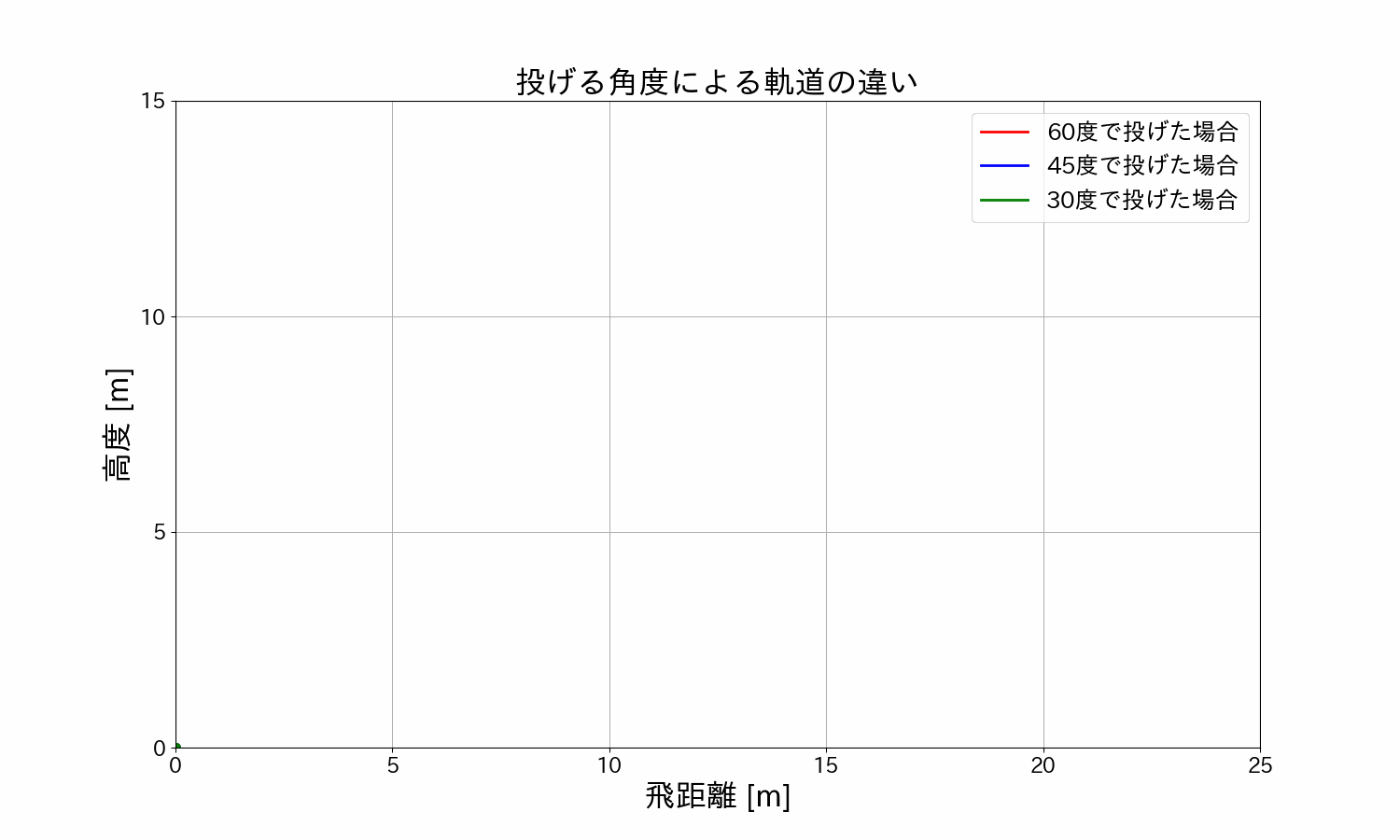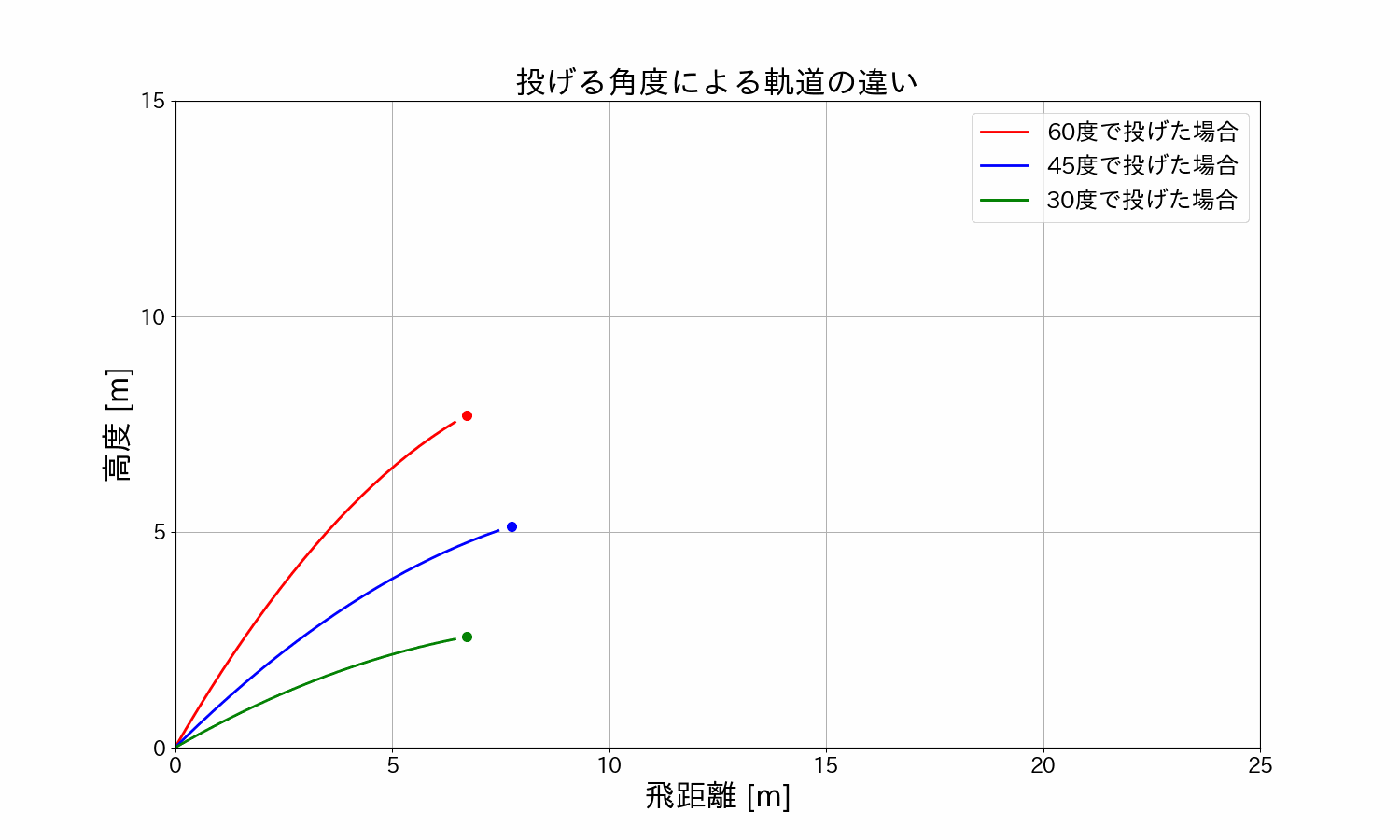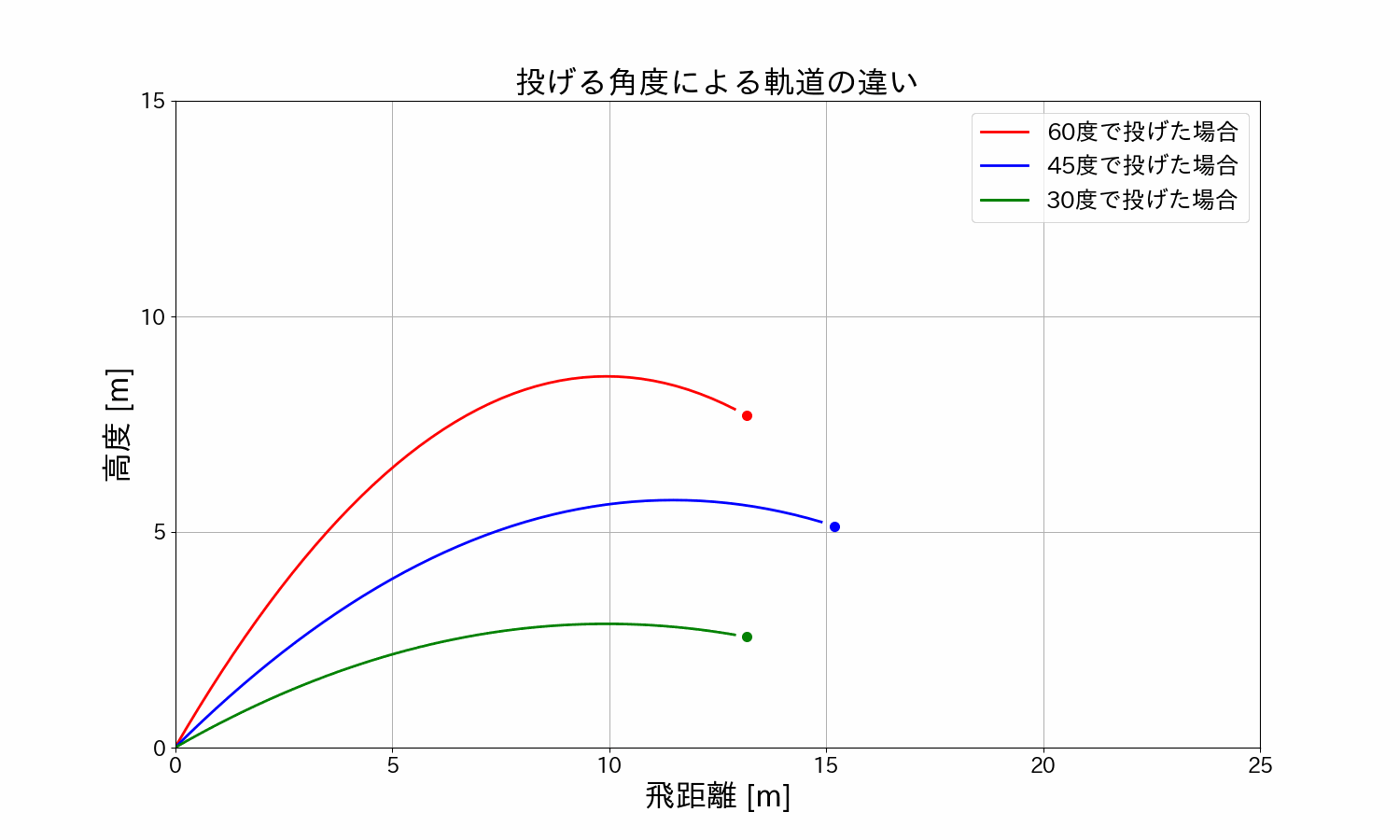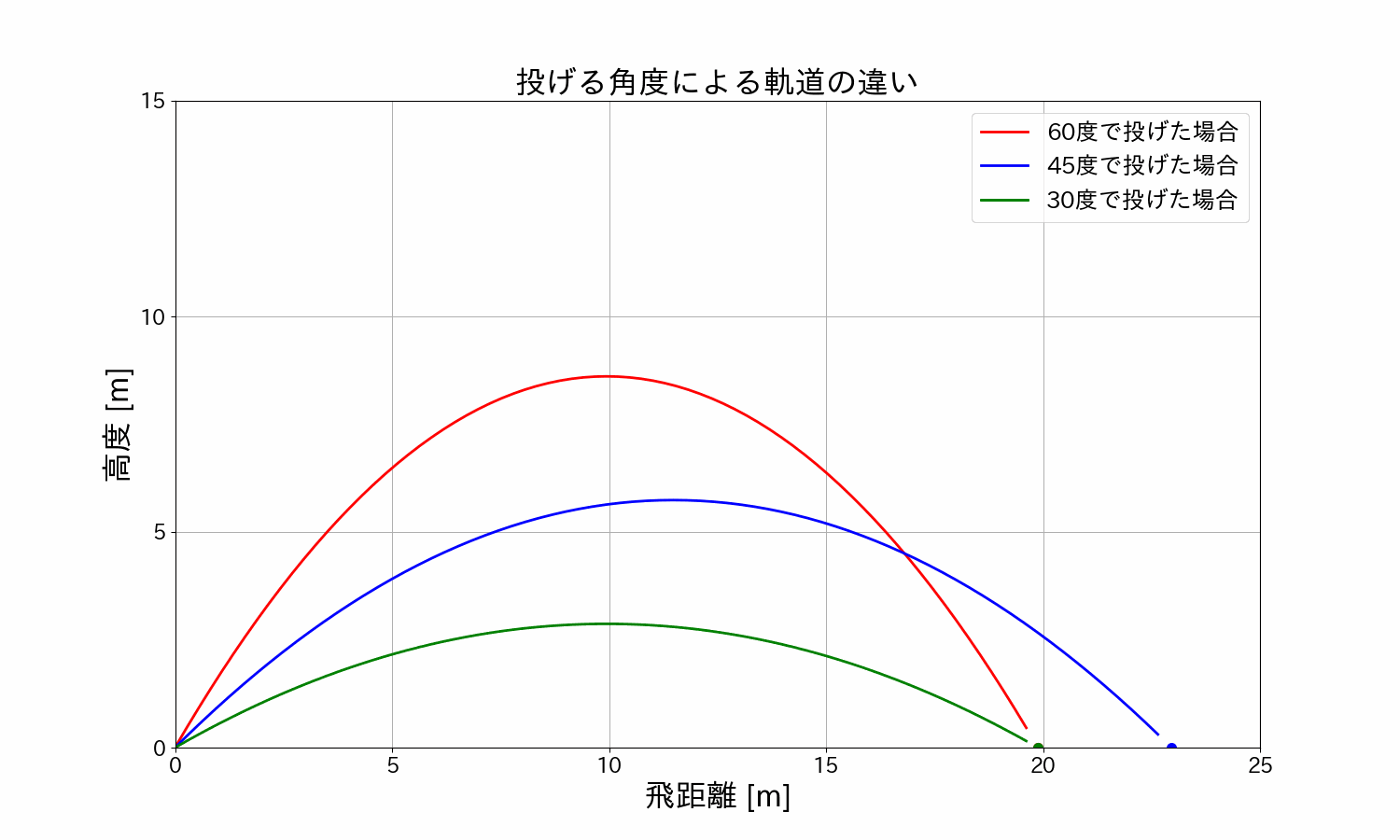
アニメーションでみると一目瞭然ですね。
\(45°\)の角度で投げたとき、飛距離が最大になることが分かります。
まとめ
本記事ではハンドボール投げをテーマに「どのくらいの角度でボールを投げれば一番遠くに飛ぶのか?」を計算しました。
さらにボールの軌道をアニメーションを用いて紹介しました。
本検討では様々な仮定を設定しており、必ずしも現実世界を完璧に表現したものではありません。
しかしながら参考程度にはなると考えています。
久しぶりにLaTeXを用いて記述しましたが、案外覚えているものですね。
また、Pythonも久しぶりに触りましたが、意外と忘れておらず安心しました。
相変わらずMatplotlibは使いやすいですね。
本記事が力は無いけれどハンドボール投げのスコアを上げたい私のような皆さんの参考になれば幸いです✨


コメント