はじめに
資産増加に関する法則
本記事は投資に関連する記事です。
投資をしている多くの人は「早く資産増えてほしい~✨」と思っているかと想像します。
本記事のテーマは、そんな資産増加に関する法則「72の法則」です。
本記事は投資に関する話題というよりは、数学要素が若干強めの内容です。
数学が苦手な方はご了承下さい。
m(_ _)m
「72の法則」とは
「72の法則」とは「ある資産を年利r%で運用した場合、何年で元本の2倍になるか」を概算するための法則です。
投資をしている人であれば一度は聞いたことがあるかもしれませんね。
例えば年利4%運用した場合、72÷4=18となり、投資元本が2倍になるのに約18年間を要することが計算できます。
ざっくりとした投資期間を算出するのに非常に便利✨
「72の法則」を証明してみる
「72の法則」の「72」って?
私は「72の法則」を聞いた時「『72』ってどこから出てきた?」という疑問を抱きました。
そこで本記事では「72の法則」を証明を試みることで、「72」の由来を考察してみたいと思います。
ここから先、やや数学要素が強めとなります。

具体例(100万円を年利4%で運用すると?)
まず「\(72\)の法則」の証明を試みるにあたり、具体的な事例で考えてみます。
仮に「\(100\)万円の投資元本を\(4 % \)の利回りで運用したとき」を考えてみます。
このとき\(1~5\)年後の金額は以下の通りですね。
| 運用年数 | 計算式(万円) | 金額(万円) |
| \(1\)年後 | \(100×(1+0.04)\) | \(104\) |
| \(2\)年後 | \(100×(1+0.04)^2\) | \(108\) |
| \(3\)年後 | \(100×(1+0.04)^3\) | \(112\) |
| \(4\)年後 | \(100×(1+0.04)^4\) | \(117\) |
| \(5\)年後 | \(100×(1+0.04)^5\) | \(122\) |

運用期間が増えるにしたがって、資産が少しずつ成長するのが分かります。
今回想定している条件では、資産は指数関数的に増加するため、運用期間が長くなればなるほど、資産増加額も大きくなります。
数十年後には元本の2倍まで膨らみそうな気がしますね。
長期投資の醍醐味です✨
「72の法則」の証明を考える
式を作る
上記の例では具体的な数値を使いましたが、少し抽象化して下のような状況を考えます。
「\(x\) 万円の資産を利回り \(r \) で \(n\) 年間運用し、投資元本が \(2\) 倍となった状況」
このような状況は数式では以下のように表現できます。
\(2x=x(1+r)^n\)
\(x\):投資元本(万円)、\(r\):利回り、\(n\):元本が2倍になるのに必要な運用期間
\(x,r,n\)は全て正の実数とします。
(投資元本や利回りが負となる運用は悲しいので、正としておきましょう😫)
数式の左辺と右辺はそれぞれ以下の状況を示しています。
左辺:投資元本 \(x\) が \(2\) 倍になった状況
右辺:\(x\) 万円の資産を利回り \(r\) で \(n\) 年間運用し続けた状況
式変形(対数を思い出そう)
どうにか立式することができましたので、この式を変形していきます。
\(2x=x(1+r)^n\)
\(x>0\)としていますので、両辺を\(x\)で割ります。
\(2=(1+r)^n\)
ここで右辺に着目すると\(n\)乗の形となっており、このままでは扱いづらいため対数を取ります。
対数の底は\(e\)にしておきます。
(\(log_{e}\)は\(ln\)と書くことも多いですが、ここでは\(log_{e}\)と記載しています。)
\(log_{e}2=log_{e}(1+r)^n\)
この式を対数の性質を活かして変形します。
(高校数学を思い出しますね✎懐かしい✨)
\(log_{e}2=n\log_{e}(1+r)\)
両辺を\(log_{e}(1+r)\)で割ります。
(\(r>0\)のため\(log_{e}(1+r)>0\))
\(\displaystyle \frac{log_{e}2}{log_{e}(1+r)}\)\(=n\)…(*)
近似式による簡略化
(*)の式において\(r\)(利回り)を決めれば、\(n\)を求めることができますね。
しかし以下のような疑問が湧いてきます。
「式が複雑すぎる…!」
「これのどこが『72の法則』なんだ!?」
「72なんて出てこないじゃないか!?」
…等々。
いずれにせよ、このヤヤコシイ式では「72の法則」のように、運用期間を簡単に(暗算で)概算するのは困難です。
そこで下の近似式を用いることにします。
近似式:\(log_{e}(1+r)≒r\) (\(r\)が十分小さい時)
この式を用いると(*)の式は以下のように超簡単になります。
\(\displaystyle \frac{log_{e}2}{r}\)\(=n\)
ここで\(log_{e}2=0.69314…\)ですので、
\(\displaystyle \frac{0.693}{r}\)\(≒n\)
となります。
「72の法則」の「72」の由来
先に示したように\(n≒\displaystyle \frac{0.693}{r}\)の式を用いれば、簡単に運用期間\(n\)を計算可能です。
しかし\(69\)は約数が\(1,3,23,69\)の\(4\)つしかなく計算に不便ですね。
そこで約数が多く計算しやすい、\(72\)が広く使われるようになったと考えられます。
もともとは「72の法則」ではなく「69の法則」だったのかもしれません。
「72の法則」の確からしさ(理論値との比較)
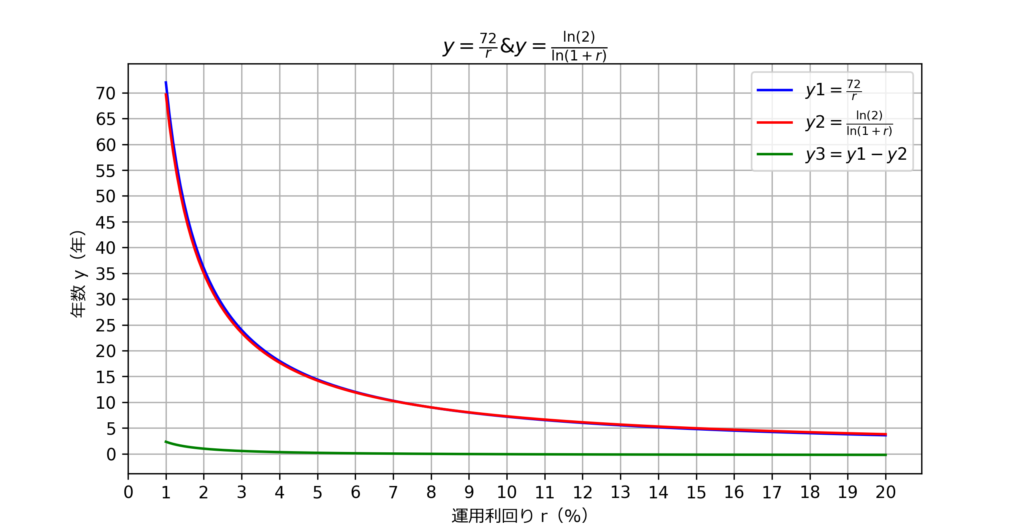
最後に「\(72\)の法則で概算した年数」と「計算で出せる正しい年数(理論値)」を比較してみます。
\(y=\displaystyle\frac{72}{r}\)と\(y=\)\(\displaystyle \frac{log_{e}2}{log_{e}(1+r)}\)のグラフを考えてみましょう。
グラフの補足説明↓
青線:「72の法則」で算出した年数
赤線:計算で出せる正しい年数(理論値)
縦軸:資産が2倍となる年数y(年)
横軸:運用利回りr(%)
グラフにすると一目瞭然ですね👀
2つの曲線がかなり重なっていることが分かります。
ちなみに緑の線は2つの曲線の差を表しています。
運用利回りが\(1\)~\(2\%\)付近では数年分の誤差が出ていますが、それ以上の利回りではほぼ0になっています。
すなわち「\(72\)の法則」の年数と理論値がほぼ等しい状態を表しているといえますね。
「\(72\)の法則」の計算過程では、近似式を用いたり、約数の少ない\(69\)から約数の多い\(72\)に変更したり、扱いやすくするための工夫をしていました。
このため精度が気になっていましたが、心配する必要はなさそうです。
補足:近似式\(log_{e}(1+r)≒r\)
ちなみに近似式\(log_{e}(1+r)≒r\)の説明ですが、数式を用いた説明では長文となるため割愛します。
代わりにグラフを載せて証明をサボったことを誤魔化しておきます。
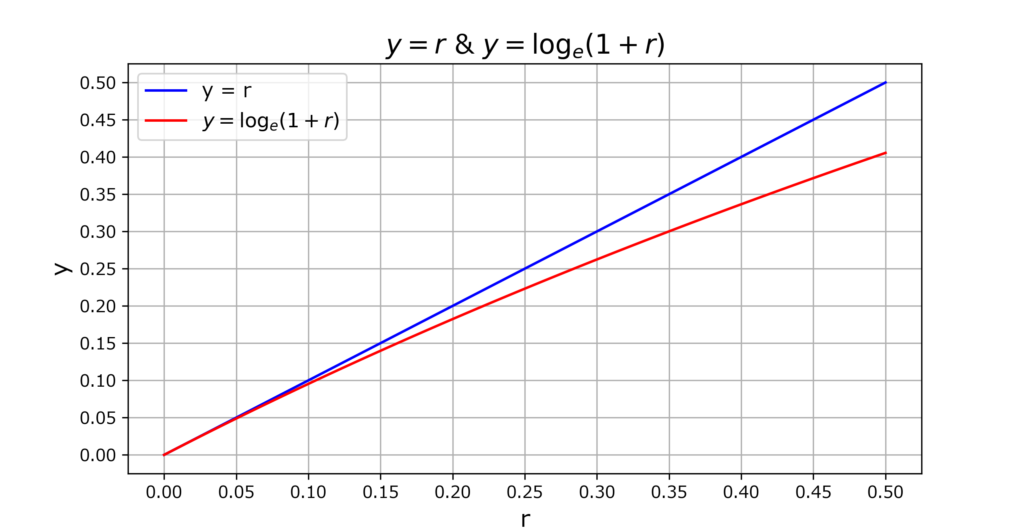
\(r\)が十分に小さい区間(グラフ左端のあたり)では、2つのグラフがほぼ重なっており、\(log_{e}(1+r)\)と\(r\)が近い値になっていることが分かります。
比較的堅実な投資を行う場合、利回り\(r\)は\(0.1\)すなわち\(10\%\)以下と十分小さいと考えることができ、近似式\(log_{e}(1+r)≒r\)を用いても問題ないと思われます。
証明してみた感想
本記事のテーマは「72の法則」でした。
投資に関する情報収集をしていると目にする法則ですね。
個人的に「72」の由来が気になったため、本記事では「72の法則」の証明にチャレンジしてみました✏️
学生時代に勉強した対数や近似式の知識を使うのは久しぶりで、懐かしい気持ちになりますね✨
また、計算を進めると「72」ではなく「69」が出てくるのは非常に興味深かったです。
数学的により厳密な「69」ではなく、約数が多く計算が容易な「72」を用いる点に「人間の都合の良さ」や「人間臭さ」を感じて面白かったです。
ちなみに本記事で示した2つのグラフは共にpythonのライブラリであるmatplotlibを用いて作成しました。凡例やグラフタイトル、軸ラベルの設定など、色々と小回りが利く便利なライブラリですね✨
数学要素が強めの本記事を最後までご覧下さりありがとうございました😌

-120x68.png)
コメント