はじめに
お久しぶりです。久しぶりに真面目な(?)内容の記事です。
本記事では複利計算について記します。
ちなみに本動画とほぼ同じ内容をYouTubeに投稿しています📹️
動画の方が好み/ながら聞きをしたい!という人にオススメです。
さて、今年から新NISAが始まり、多くの人が投資に勤しんでいると思いますが、多くの人にとって、投資の目的は「お金を増やすこと」になると思います。
そこで投資でどれくらい増えるのか調べてみると、「年利◯%で毎年◯◯円積み立てれば◯年後に〇〇〇円になる!」という記事によく出会います。
ですが、そのような記事では計算式がなく、結果だけが示されており、正しいのかも分からない…というケースも多いです。というわけで、本記事では投資成績のシミュレーションにも使える複利計算について記します。
複利と単利の違い
まずはじめに「複利計算」の「複利」ついて記しておきます。似たような言葉で「単利」があります。両者の違いについて簡単に述べると以下のとおり。
単利:元本のみに対して利息が発生
複利:元本+利息に対して利息が発生
投資に当てはめると、複利では利息に対しても利息が付くため、雪だるま式にどんどん資産が大きくなっていきます。
複利計算について
毎年100万円積立・想定利回り3%で運用するケース
単利と複利の違いを確認したところで、次は複利計算について記します。
イメージしやすいよう「毎年100万円積立、想定利回りは3%」というケースを想定します。
この仮定のもとで各年における資産額を試算します。(”しさん”がくを”しさん”…!)
(計算しやすいよう、資産が増加するのは年初とし、計算では千円の位を四捨五入します。)
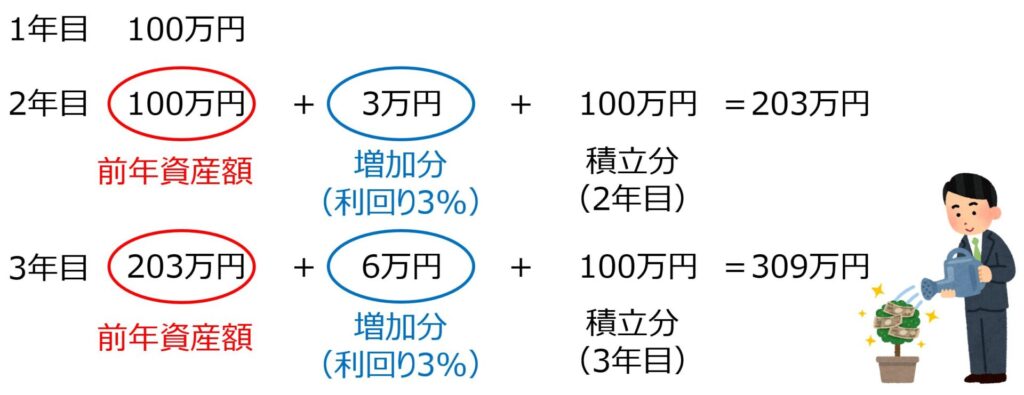
まず、1年目が終了時点の資産は100万円となります。
つぎに2年目が終了時点の資産は203万円となります。
1年目の100万円+増加分3万円=103万円と2年目に積み立てた100万円を合わせた金額です。
増加分3万円は100万円×利回り3%で求めています。
そして3年目終了時点の資産は309万円となります。
2年目の203万円+増加分6万円=209万円と3年目に積み立てた100万円を合わせた金額です。
増加分6万円は203万円×利回り3%で求めています。
まだこのあたりですと”複利の力”はそれほど感じませんね。
計算が少しずつヤヤコシクなってきましたので、次章で一般化(抽象化)したいと思います。
一般化(等比数列の和の公式)
さて、先程までの内容を一般化します。すなわち「毎年a円積立、想定利回りr%」というケースを想定します。この時、資産額の推移は以下のようになります。
1年目:\(a\) 円
2年目:\(a×(1+r)+a\) 円
3年目:\(a×(1+r)^2+a×(1+r)+a\) 円
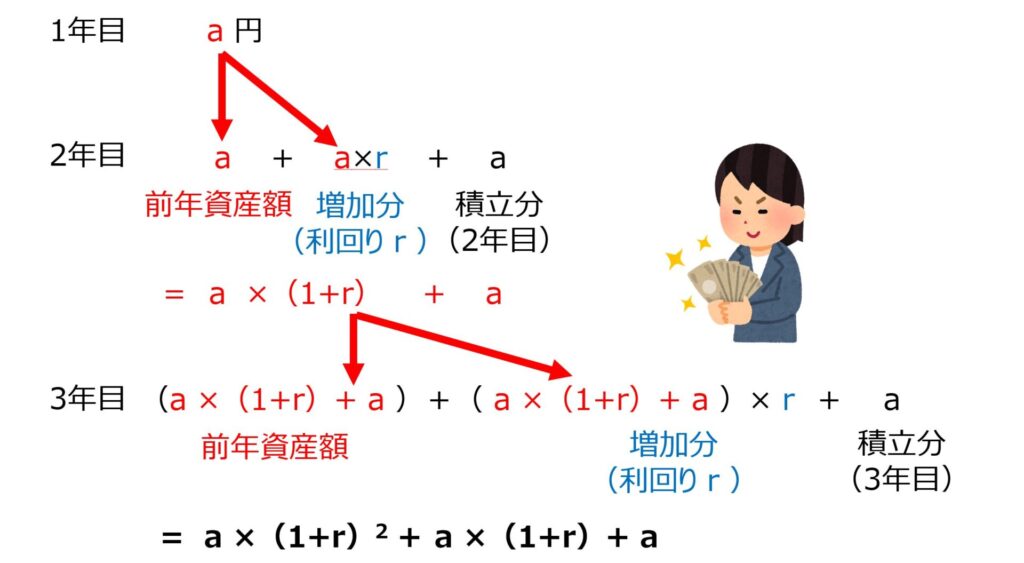
この式をよく見てみると、等比数列の形をしています。
そこで等比数列の和の公式を用いて、ある年の資産額を求めてみることにします。
ちなみに等比数列の和の公式は以下の通り↓
初項が\(a, \)公比が\(r, \)項数が\(n\)の等比数列の和\(S\)は、
\(S=\displaystyle\frac{a(1-r^n)}{1-r}\)
(ちなみに公比\(r=1\)の時、\(S=na\)です。)
この公式を使えば5年目、10年目、20年目の資産額も簡単に求めることが出来ます。
めちゃ便利!!
先程の例に当てはめてみると、初項(a)は100万円、公比(r)は1.03(想定利回り3%)ですね。nには年数を代入すればokです。
以下が資産額の試算結果です。
| 積立年数 | 資産額 (万円) | 備考 |
| 5 | 531 | n=5 |
| 10 | 1,146 | n=10 |
| 15 | 1,860 | n=15 |
| 20 | 2,687 | n=20 |
| 25 | 3,646 | n=25 |
せっかくなのでグラフにしてみました。
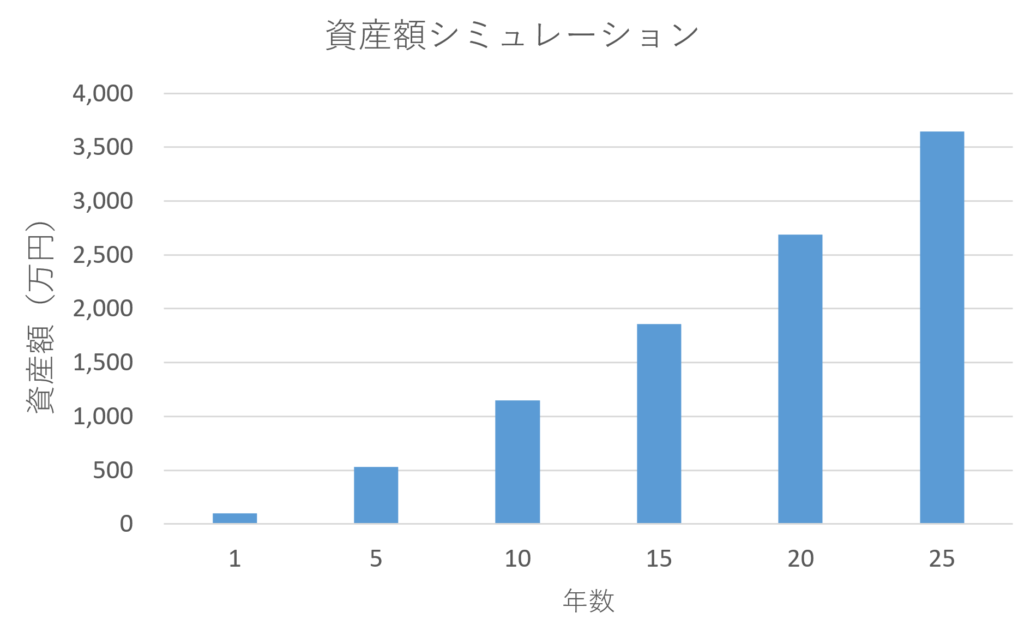
時が経つにつれ急激に資産が増加するのが分かります。
具体的には、
5年目→10年目の増加額は615万円ですが
15年目→20年目の増加額は959万円と資産の増えるスピードが加速しています。
これが利息にも利息がつく複利の威力ですね。
実際の株価は乱高下しますので、シミュレーション通りにはなりませんが、イメージは掴めるかと思います。
以上が複利計算に関するお話でした。投資でお金を増やすには、時間を味方にすることが重要ですね。次回は本記事の議論を踏まえて「5年早く投資を始めた人に追いつくには」について記します。(たぶん。)
今回の記事ではLaTeXを使用して式を記述してみました。LaTeXは学生の頃に習いましたが、使い方をすっかり忘れていました、LaTeXを「ラテフ」と読むのはギリギリ覚えていましたが…。


コメント